Selectionsort is a simple sorting algorithm with a quadratic running time (O(n2)).
How it works
Basic idea:
The array consists of a sorted part followed by a not yet sorted part. The fields in the sorted part contain the elements that the sorted array will also contain after the execution of the algorithm. Before the i-th iteration, the sorted part consists of the first i-1 elements of the array. After the i-th iteration, the i-th field of the array should contain the smallest element from the unsorted part. Thus, after the i-th iteration, the first i fields contain the correct elements.
This is achieved by searching all elements from the unsorted part for the smallest element in each iteration, and if the i-th element is not the smallest element, the smallest and i-th elements are swapped.
Suppose the array looks like this after the second iteration:
The first two elements are already in the correct field. In the 3rd iteration the unsorted part of the array (the white fields) is searched for the smallest element. This is the 3. So the 3 and the 8 are swapped. After that the first 3 elements are at the right position.
Pseudocode:
Procedure:
It is iterated with an index i starting from 0 over all fields of the array (except the last field). In each iteration, the element with index i is first the smallest element found in the unsorted area. Then, with the help of an index j, iteration is performed over all fields behind the i-th field and each time the element with index j is smaller than the smallest element found so far, the element with index j becomes the new smallest element found.
If after iterating over all elements out of the unsorted part the smallest element is not yet at position i, the smallest element and the element at position i are swapped.
If there is only one element left in the unsorted area, it is also automatically in the correct position and the algorithm can be terminated.
small example:
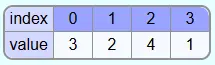
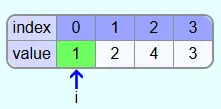
As an example, the following array is to be sorted with Selectionsort:
Iteration 1:
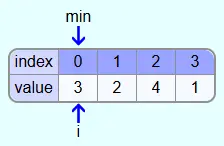
In the first iteration i=0 (value 3). The first element at the beginning of this iteration also becomes the smallest so far found element min.
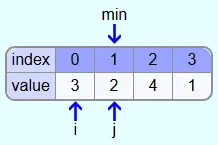
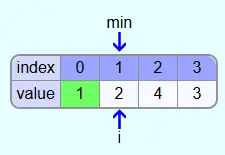
Then we iterate with index j over all the fields behind the field with index i. First it is checked whether the element with index 1 is smaller than the element at position min. This is the case (2<3) and thus the element with index 1 is the new smallest element.
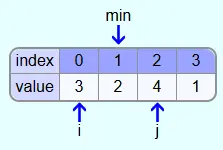
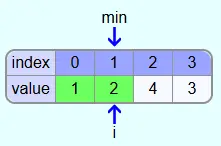
Then the elements with indices 1 and 2 are compared. Since 4 is not smaller than 2, no new smallest element was found.
Since 1 is less than 2, min is assigned index 3 in the next step.
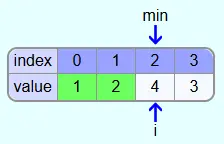
The smallest element found is not yet at position i. So the element at position i and the element at position min are swapped.
The sorted part of the array now consists of the field with index 0 and the unsorted part of the array consists of the fields with indices 1-3.
Iteration 2:
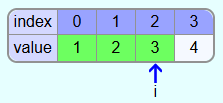
Next, the element in the field with index 1 becomes the new smallest element.
Since 2 is smaller than 4 and 3, min is not changed after comparison with the elements with indices 2 and 3. Thus, the correct element is already in the field with index i and no elements have to be swapped in the iteration.
Iteration 3:
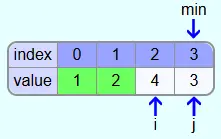
In iteration 3, the indices i and min are set to 2.
Since 3 is less than 4, the element with index 3 becomes the new smallest element with index min.
The field with the index i does not yet contain the smallest element. So the 3 and the 4 are swapped.
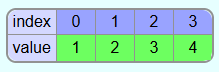
Result:
The unsorted range now contains only 1 element and a single-element subrange is always automatically sorted. Thus, the entire array is now sorted.
Reverse sort order
The selectionsort algorithm can be easily adapted so that the elements are not sorted in ascending order, but in descending order starting with the largest element. For this purpose, the largest element rather than the smallest element must be searched for in the unsorted area.