Prim's algorithm receives a graph G=(V, E) and creates from it a minimum spanning tree G'=(V, E').
What is a minimum spanning tree?
Suppose G=(V,E) is an undirected and connected graph. G' is a spanning tree, if:
- G' contains exactly the nodes that are also contained in the graph G
- G' contains only edges that are also contained in G
- G' is connected and free of cycles
If there is no spanning tree of G, where the sum of the edge weights is smaller than the sum of the edge weights of G', then G' is a minimum spanning tree of G.
Example:
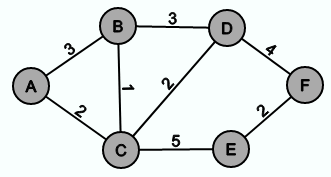
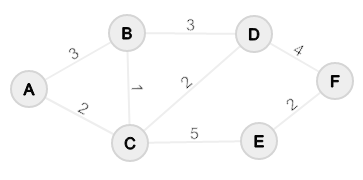
Assume that the graph looks like this:
A minimum spanning tree in this case looks like this:
The following graph is a spanning tree of the example graph, but since the sum of all edge weights is 14 and there is a spanning tree where the sum of edge weights is 11, it is not a minimum spanning tree.
The following graph is not a spanning tree because it contains a cycle and is not connected:
Basic principle
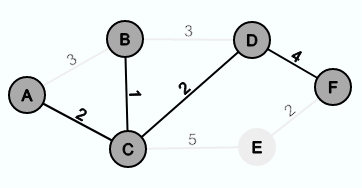
Again, the graph from the above chapter will serve as an example. One first chooses a node from G as the start node and inserts it into G'.
In each iteration, one selects the edge with the smallest weight that connects a node in the new graph G' and a node that is not yet in G' with each other and inserts both the edge and the node that is not yet in G' into G'.
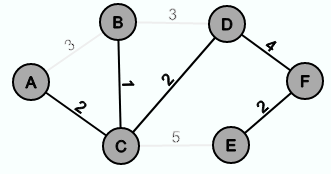
So it can be decided between the edge {A,B} and the edge {A,C}. Since the edge {A,C} has the smaller weight, the node C and the edge {A,C} are inserted in G'.
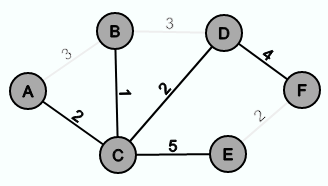
Next, you can decide between the edges {A,B}, {C,B}, {A,B}, {C,D} and {C,E}. Since the edge {C,B} has the smallest weight, you choose this one.
Next, you can decide between the edges {B,D}, {C,D} und {C,E} and one chooses {C,D}.
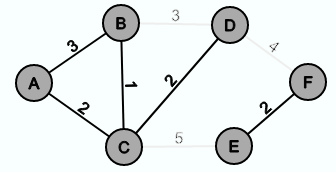
After that one selects {D,F}.
And lastly {F,E}.
In principle, Prim's algorithm works as described in this chapter, but the above description was somewhat simplistic.
How it works
Pseudocode
Input:
The prim algorithm obtains an undirected and cycle-free graph G=(V,E,start), where V is the set of nodes, E is the set of edges and start is the start node.
Important values and sets:
Q: A set of nodes Q is required. This contains the nodes that have not yet been added to the spanning tree. It is useful to use a priority queue for this purpose.
distance[v]: For each node v∈V the distance to the present spanning tree is stored.
predecessor[v]: For each node, a parent element is stored.
E and E': E is the set of all edges of the input graph and E' is the set of edges of the evolving minimum spanning tree.
Goal:
After running the prim algorithm, E' contains all edges of a minimum spanning tree of G. Since a spanning tree contains all nodes of the initial graph, there is no need to create an additional set for the nodes.
Initialization:
The start node gets assigned 0 as distance value, all other nodes ∞.
All nodes are assigned null as predecessor.
All nodes are inserted into Q.
Loop:
In each loop iteration, the node u with the smallest distance to the evolving spanning tree is extracted from Q. Then, for each neighbor v∈Q of u, one looks at whether the distance between u and v is smaller than the distance between v and the present evolving graph. If so, distance[v] and predecessor[v] are adjusted.
Example
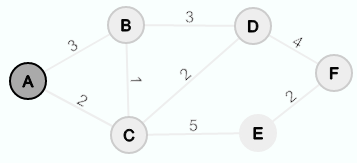
As an example we will use the graph from above with A as starting node:
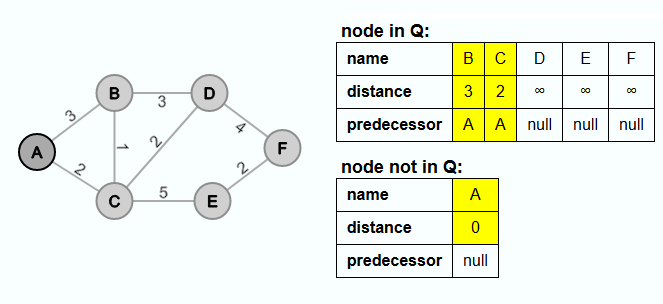
In the initialization phase of the prim algorithm all nodes are inserted into Q and all nodes get null assigned as predecessor. The start node is initialized with the distance value 0, all others with ∞.
The starting node A is the node in Q with the smallest distance value. So A is extracted from Q.
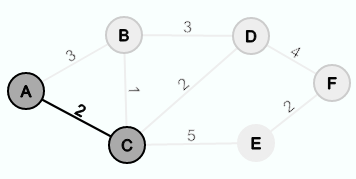
A becomes the predecessor of B and C and the distance values are adjusted. Since A is the starting node, no edge is inserted into E'.
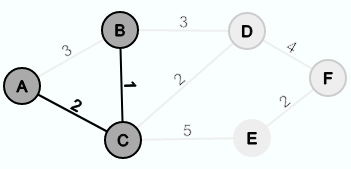
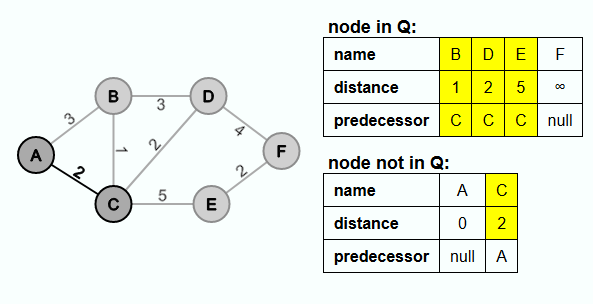
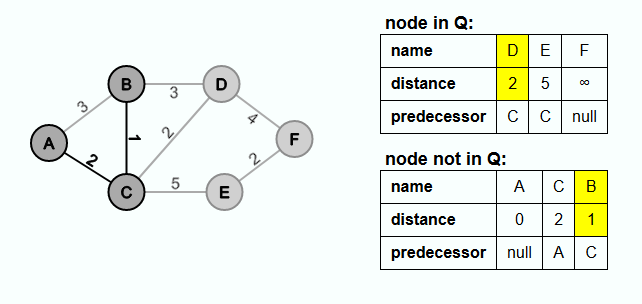
Next, C is extracted from Q and the edge {A, C} is inserted into E'. The distance from C to B is less than the distance value stored for B. Thus, the distance value is set to the weight of the edge {C, B} and C becomes the new predecessor. Since no connection to the evolving minimal spanning tree has yet been found for E and F, the distance and predecessor are also adjusted by these nodes.
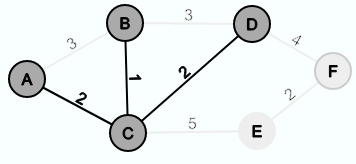
Then B is extracted from Q and the edge {C, B} is inserted into E'. The distance to D is not smaller than the stored value, so nothing else is done in this iteration.
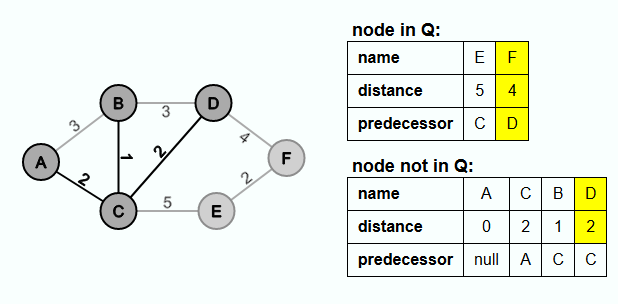
Now D is extracted from Q and the edge {C, D} is inserted into E'. The first connection to F was found. So D becomes the new predecessor node of F and the distance is set to 4.
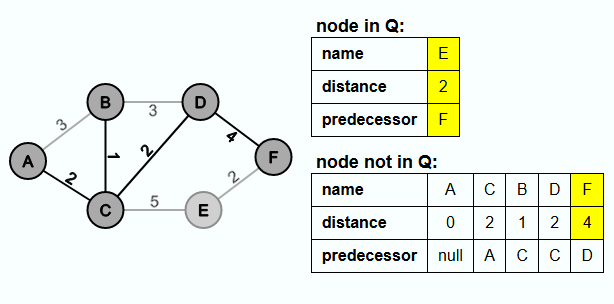
Then F is extracted from Q and the edge {D, F} is inserted into E'. Since the distance to E is less than 5, F becomes the new predecessor of E and the distance value of E is set to 2.
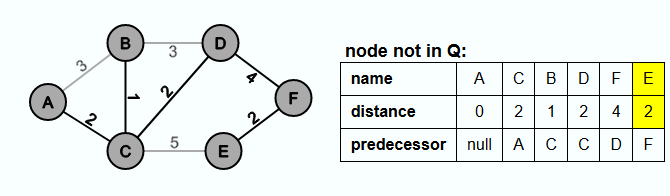
In the last iteration the node E is extracted from Q and the edge {F, E} is inserted into E'.