Mergesort is an efficient sorting algorithm that splits the list or array into smaller and smaller lists or arrays, which are later reassembled in sorted order.
How it works
Basic idea:
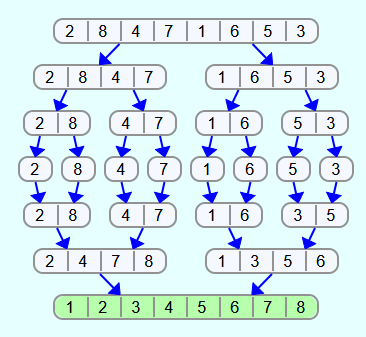
In the Mergesort algorithm, the list to be sorted is first divided into 2 new lists. These lists are sorted recursively with Mergesort. Afterwards, the two sorted lists are merged into one list again.
Pseudocode:
Procedure:
If the list that is used to call Mergesort contains less than 2 elements, the list is automatically sorted. In this case, nothing needs to be changed in the list.
If the list contains more than one element, the list is split into a left and a right list. If possible, the same number of elements should be inserted into both new lists. If the number of elements is odd, 1 more element is inserted into one of the two new lists than into the other one.
Mergesort is then applied recursively to the two new lists, so that the two lists are sorted after each of these calls.
Then the two sorted lists must be merged. For this, the foremost element from both lists is always considered. If the foremost element from the left list is smaller than the foremost element from the right list, then the foremost element from the left list is removed from the list and inserted at the back of the output list. And if the first element from the right list is smaller than the first element from the left list, then the element from the right list is removed and added to the back of the output list. This will be repeated until one of the two lists is empty. If this is the case, then the remaining elements from the not yet empty list are inserted at the end of the output list. When this is done, the output list is sorted.
Example
Als Beispiel soll die folgende Liste sortiert werden:
First, the list is divided into 2 lists.
Then the mergesort algorithm is applied to the two lists. This results in 2 sorted lists.
These lists are to be combined into one list.
For this purpose, the first two elements of the 2 lists are compared and the smaller number is removed from the list and inserted into the result list at the back. Since 1 is smaller than 2, 1 is removed from list 2 and inserted into the still empty result list.
Again, the first two elements are compared and since 2 is less than 3, 2 is removed from list 1 and appended to the result list.
And that is how it continues until one of the two lists is empty.
List 2 is now empty. This means that the two remaining elements from list 1 can be inserted into the result list without having to compare them with an element from list 2.
The list is sorted now.
In the example, only one call of Mergesort was gone through, but the principle is exactly the same with the two lists that are created in the "dividing phase" and to which Mergesort is applied recursively. The lists are split into smaller and smaller lists until the lists consist of only one element and then reassembled into sorted lists.