Insertionsort is an algorithm for sorting lists and arrays. The sorting algorithm is very efficient for arrays that are already pre-sorted to a large extent.
How it works
Basic idea:
The array is divided into a sorted part followed by an unsorted part. Unlike, for example, Selection Sort or Bubble Sort, the elements from the sorted section have potentially not yet reached their final position. In the insertionsort algorithm, the foremost element from the unsorted range is sorted into the sorted range in each iteration. This is achieved by searching for the position where the element is to be inserted, moving all larger elements 1 field to the right to make room for the element to be inserted, and then inserting the element to be inserted at the position found.
For example, before an iteration step, the array should look like this:
The bluish fields are the sorted part of the array and the white fields are the unsorted part. Next, the foremost element from the unsorted area should be sorted into the sorted area. This is the 6. The 6 belongs between the 5 and the 7. So that the 6 can be sorted in, the 7 and the 8 must be moved first in each case 1 field further to the right.
After the iteration step the array looks like this:
Pseudocode:
Procedure:
Before each iteration of the outer loop, the sorted range consists of the elements with indices 0 to i-1 and the element at position i is to be sorted into this subrange. Since a one-element subarray is automatically sorted, the array can start with i = 1 instead of i = 0.
j is the index of the field for which it is currently being checked whether it is a field into which the element to be inserted can be inserted so that the sorted part is still sorted afterwards. At the beginning j is set to the index of the first element behind the sorted part. So to the field of the element which should be sorted.
Since the field containing the element to be inserted can be overwritten in the inner loop, the value to be inserted is cached in the variable "toInsert".
The inner loop is used to search for the index at which the element is to be inserted. For this, the element to the left of position j is always considered. If the element with index j-1 is larger than the element to be inserted, then it is moved to the right to make room for the new element to be inserted. Then j is moved 1 more to the left. This is done until j either reaches the beginning of the array or until the element in the field before j is smaller than the element to be inserted. If this is the case, j is the position where the element will be inserted.
Example
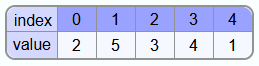
As an example, the following array is to be sorted:
Iteration 1:
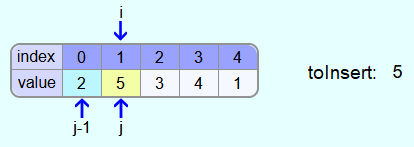
Before the first iteration, only the first element, i.e. the 2, is in the sorted area. The 5 is to be sorted in. So j is set to index 1 and the 5 is stored temporarily.
Now the 2 is compared with the 5. Since the 5 is larger, the 5 is already in the correct position.
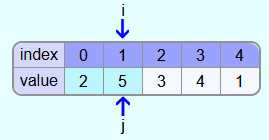
Iteration 2:
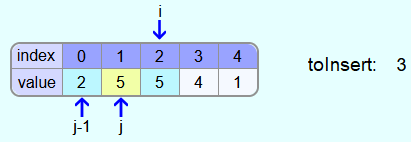
Next, the 3 is to be inserted into the sorted area.
This time the element at position j-1 is larger than the element to be inserted and thus the 5 must be copied into the field at position j. Then j is moved one field further to the left.
As you can see on the image, the 5 is now in the field with index 1 as well as in the field with index 2. But this is not bad, because the 5 in the field with index 1 will be overwritten either by the number in the field with index 0 or by the number to be inserted.
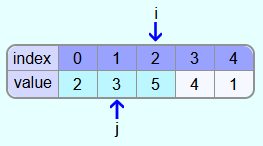
Since 2 is not greater than 3, the 3 is entered in the field with index 1.
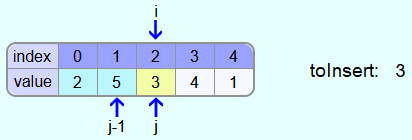
Iteration 3:
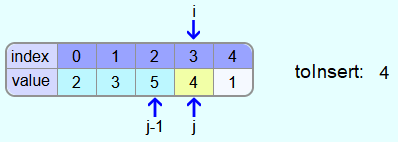
Next, the 4 is to be inserted.
The 5 is larger than the 4. Thus, the 5 must be copied one field further to the right and j is decreased by 1.
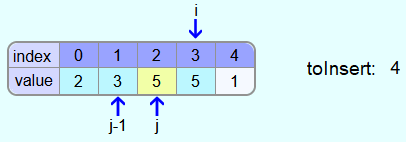
The 3 is not greater than the 4 and therefore the 4 must be entered in the field with the index 2.
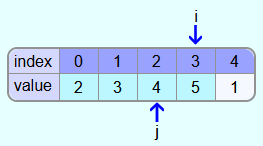
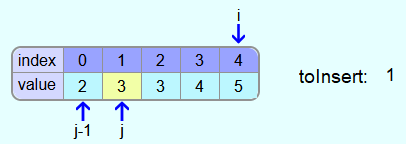
Iteration 4:
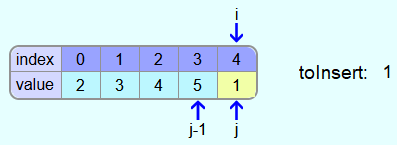
The last number to be inserted into the sorted range is 1.
The 5 is larger than the 1 and thus the 5 is copied one more field to the right.
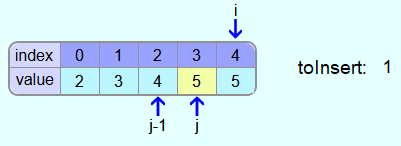
The 4, the 3, and the 2 are also all greater than 1, and so they are also all copied one space to the right, one after the other.
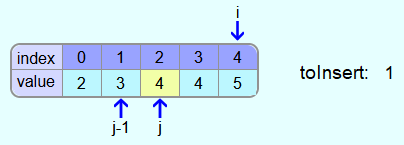
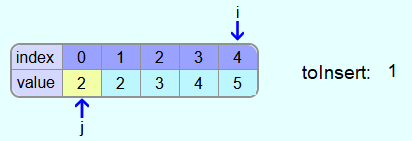
Now there is no more field to the left of j and so the 1 is entered in the leftmost field.
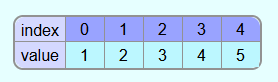
The array is now sorted.
Runtime complexity
Assume that the array is sorted the wrong way round. Then the entire sorted range must be traversed once in each iteration by the Insertionsort algorithm. This leads to a quadratic runtime complexity.
If, on the other hand, the array is sorted the right way around, the correct place to insert each element will be found on the first try, which means that the runtime complexity in this case is linear.
On average, the runtime complexity is quadratic.
The algorithm is very efficient for arrays where most of the elements are already sorted.