In the heapsort algorithm, the array to be sorted is converted into a heap. These have the advantage that they can be used to determine the largest or smallest element very efficiently, which can lead to great performance advantages when sorting. Heapsort has a runtime complexity of O(n·log n).
What is a heap?
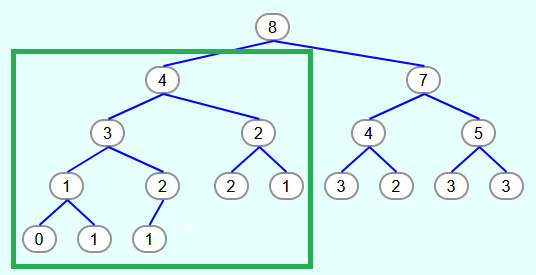
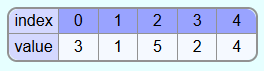
A heap is a data structure in which elements can be stored. Heaps are special binary trees in which all levels, except possibly the lowest, are completely filled with elements. If the lowest level is not completely filled with elements, the lowest level is filled from the very left to a certain position.
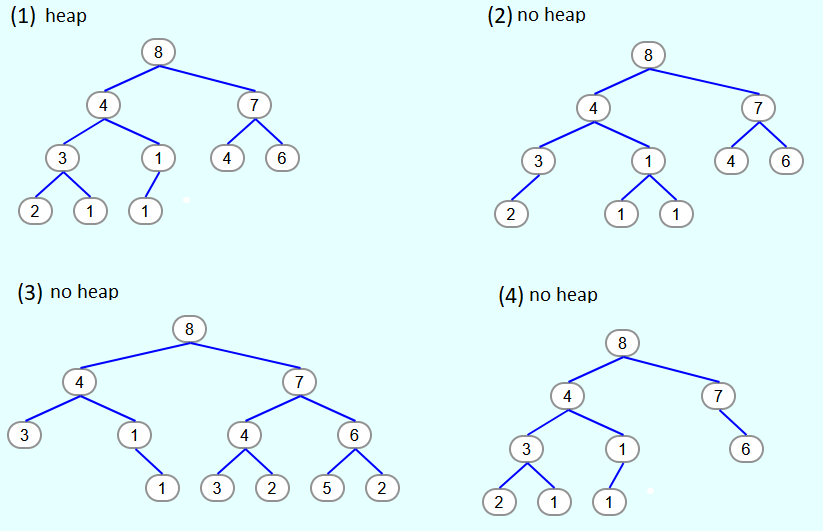
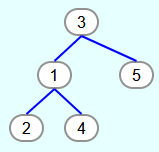
The first tree is a heap because the top 3 levels are completely filled and in the lowest level the elements were filled from the very left and without gaps.
The second tree is not a heap because the second element from the left is missing in the lowest level.
Tree 3 is not a heap because in the lowest level the elements were not filled from the left.
The fourth tree is not a heap because one element is missing in the third level and thus not only the lowest level is incomplete.
Heap property:
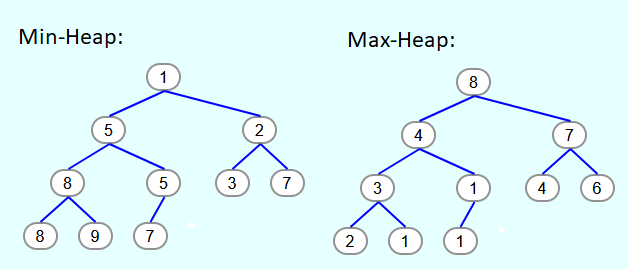
A distinction is made between min-heaps and max-heaps. In min-heaps, each element is less than or equal to its child elements, and in max-heaps, all elements are greater than or equal to their child elements. In particular, in a min-heap there is no element that is smaller than the top element and in a max-heap there is no element that is larger than the top element.
Heaps and arrays:
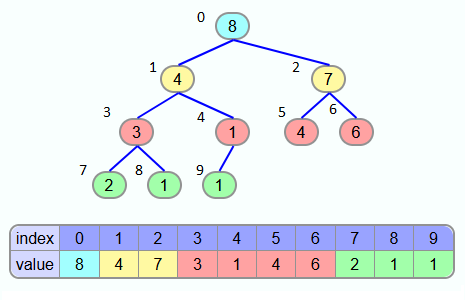
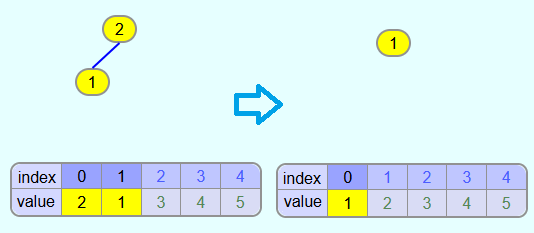
In practice, heaps are often not implemented as a tree structure, but with the help of an array. The tree structure serves as a mental model. In the array, the field with index 0 contains the top node of the tree structure. In the following fields are the two child nodes of the topmost element. In the following fields are the 4 elements from the third level of the tree structure and then from the fourth level and so on. The elements from one level are always in the same order in the array as they appear in the level of the tree structure. Always from the leftmost element to the rightmost element.
Index child node: The child nodes of an element with index i are in the fields 2·i+1 and 2·i+2. For example, the child nodes of the element with index 3 are in the fields 2·3+1 = 7 and 2·3+2 = 8.
Index parent node: To calculate the index of the parent node of an element with index i, you have to calculate (i-1)/2 and round down the result.
How heapsort works
In the following, an array is to be sorted in ascending order using the heapsort algorithm and a max-heap is used. However, sorting the array in descending order would work equivalently by using a min-heap.
Basic idea:
First, the array is converted to a max-heap where the max-heap property (each node is greater than or equal to its child nodes) is satisfied. When this is done, the largest element is in the root. This element is swapped with the last element in the heap and then removed from the heap. Now that the element in the root is potentially no longer greater than or equal to the child nodes, the heap property must be restored. When this is done, the root again contains the largest element. This is again swapped with the last element in the heap and removed from the heap, and then the heap property is restored again. This is done until all elements have been removed from the heap and are sorted in the output array.
Heapify method
To achieve this, a helper method "heapify()" is needed. This method gets the heap (as an array), the index of the root of a subtree of the heap for which the heap property is to be satisfied and the index from the last element in the heap. The method assumes that all descendants from the root of the subtree are greater than or equal to the child nodes. However, the root of the subtree may be smaller than its child nodes before the call. After the call, the max-heap property should apply to the entire subtree.
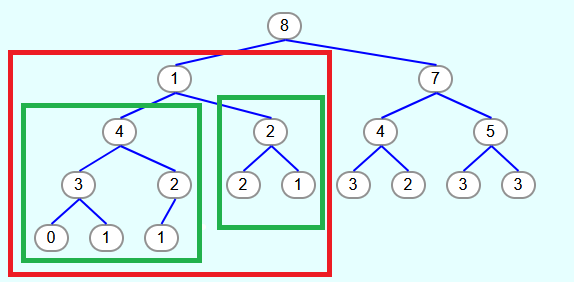
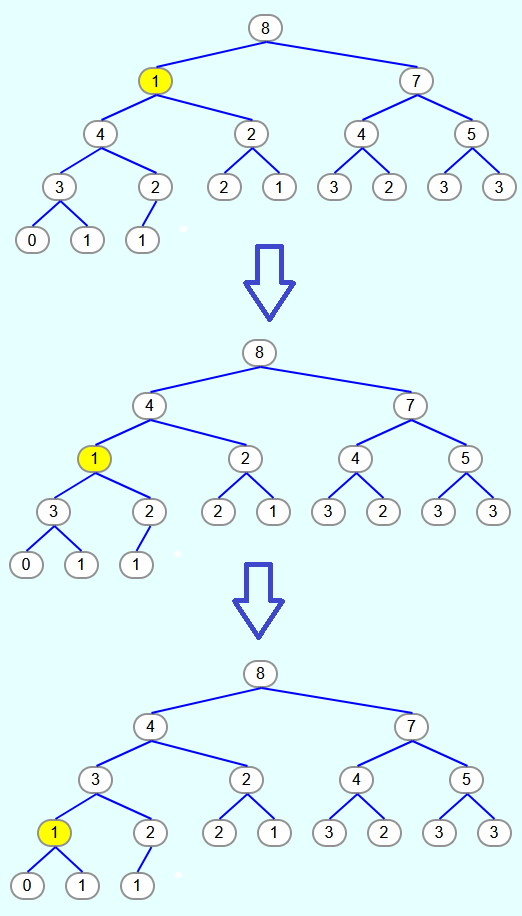
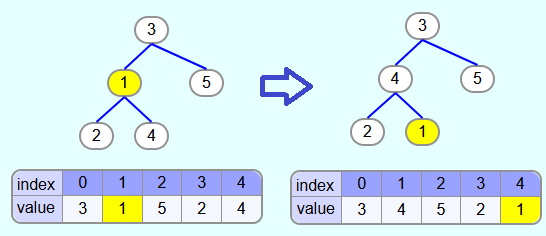
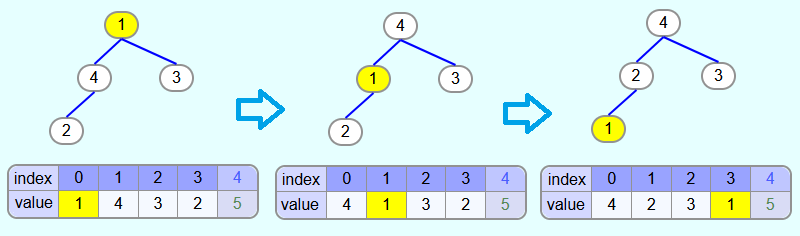
As an example, the following tree calls the heapify method with index 1.
Thus, the subtree framed in red is to be converted to a max heap. The prerequisite is that the max-heap property applies to the subtrees to the left and right of the element with index 1 (framed in green). This is the case. However, the element with index 1 does not necessarily have to be greater than or equal to the child nodes.
After calling the heapify method, the heap should look like this:
This is achieved by swapping the element that was originally in the root of the subtree (in this case the 1) with its largest child node until it no longer has a child node that is larger than the element to be "heapified" itself.
In the above example, the node with index and value 1 has child nodes with values 4 and 2. Thus, the 1 is swapped with the 4. Then the 1 has child nodes with the values 3 and 2. So the element is swapped with the 3. After that, the child nodes have the values 0 and 1. Since neither value is greater than 1, the 1 is now at the correct position.
Procedure:
Build heap: First, the heap is built. To do this, the array is reordered so that the heap property is satisfied (all nodes are greater than or equal to its child nodes). For this purpose, the heapify method introduced above is used. For each node, which has at least one child node, the heapify method is called. Due to the precondition of the heapify method, it is important to start with the last node and work upwards level by level until the heapify method is called for the root. To determine the last node, which has at least one child node, the length of the array is divided by 2 and the result is rounded down and decreased by 1 (round_down(A.length/2)-1).
Remove largest element from heap: After the heap has been built, the largest element is in the root. This is to be inserted at the end of the output array and deleted from the heap. Instead of creating an extra array for this purpose, the array that is also used for the heap can be used. In the front part of the array the elements of the heap are stored and in the back part the sorted array is created. In each iteration of the second loop, the top element (the largest) is swapped with the last element of the heap. After that, it is no longer considered to belong to the heap, but to the sorted array.
Restore heap property: After swapping the largest element and the last element in the heap and removing the largest element from the heap, the new root element is potentially smaller than at least one of the child nodes. To restore the max heap property the heapify method must be called with the index of the root (i.e. 0). Since the field with index j is now no longer part of the heap, the method is passed j-1 as the index of the last element of the heap.
The steps "remove largest element from heap" and "restore heap property" are repeated alternately until the heap contains only 1 element. Since a single element is automatically sorted, the entire array is then sorted.
Small example
The following array is to be sorted using the heapsort algorithm:
When represented as a heap, it looks like this:
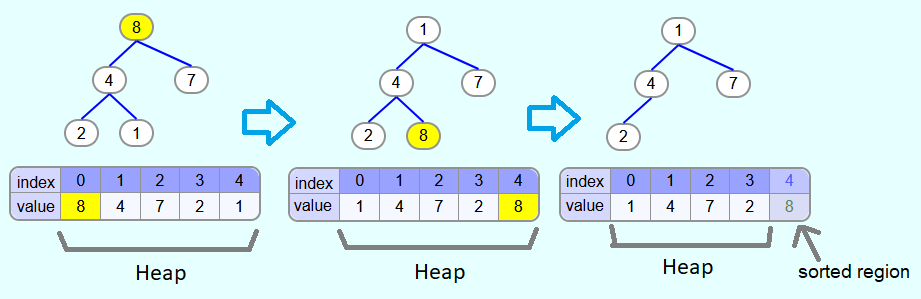
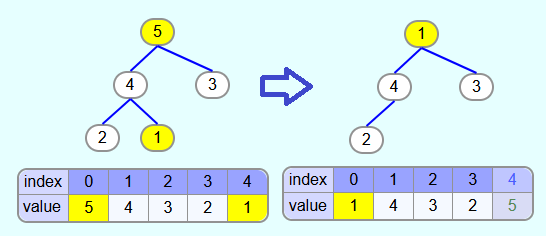
Initialization - Build heap:
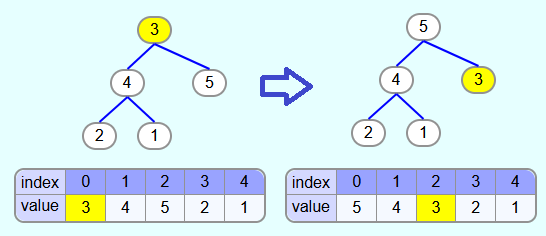
There are only 2 nodes with child nodes. First heapify method is called with index 1. Since the 1 has larger child nodes, it is swapped with the largest child node (i.e. the 4).
Then the heapify method is called with index 0. Since the 3 is smaller than the 5 and since 5 is larger than 4, the 3 is swapped with the 5.
The max-heap property is now fulfilled.
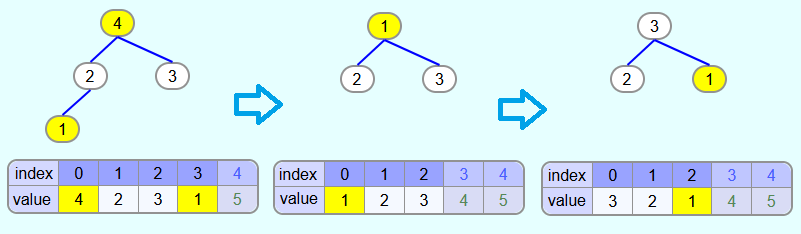
Iteration 1:
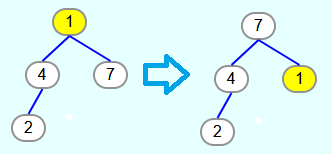
The root is swapped with the last element and removed from the heap.
The 1 violates the heap property. To restore it, the 1 must be "heapified". The 4 is the largest child node and thus the 1 is swapped with the 4. Then the 1 is swapped with the 2.
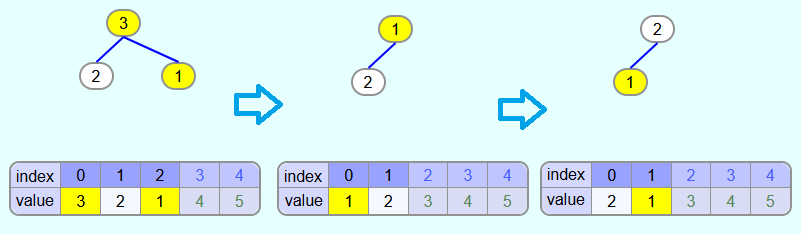
Iteration 2:
Next, the 4 is swapped with the last element and removed from the heap. After that, the 1 in the heapify method is swapped with the largest child node (i.e. the 3).
Iteration 3:
Iteration 4:
Result:
Since there is only 1 element left in the heap, it is automatically in the right place and the array is sorted.