The sieve of Eratosthenes is an algorithm that can be used to determine all prime numbers up to a given number. This number is referred to as N hereafter.
On this page you can visualize the sieve of Eratosthenes for numbers up to 1000.
How it works
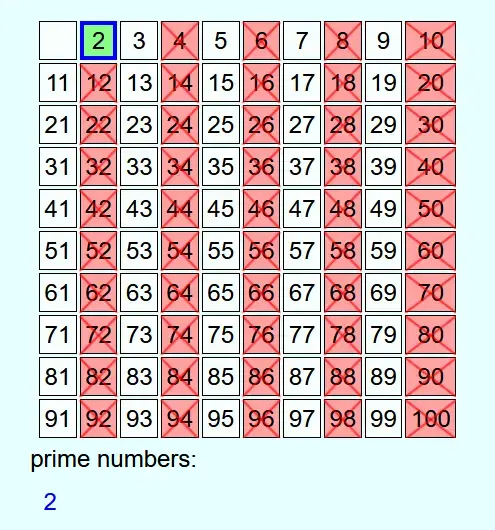
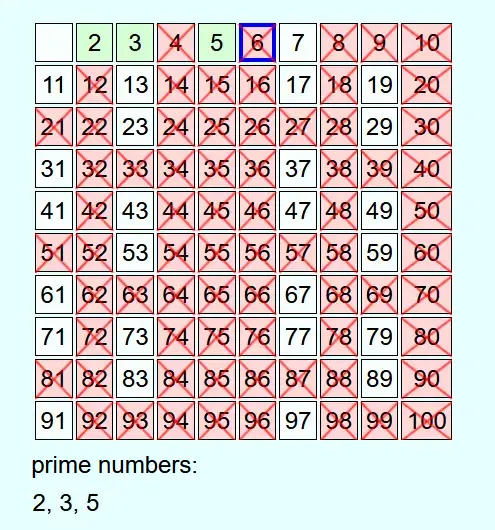
First, all the numbers from 2 to the predefined number N are written down. Then, starting from 2, go through the numbers in ascending order.
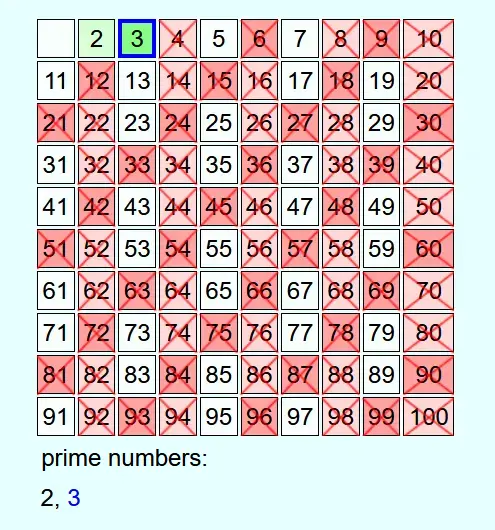
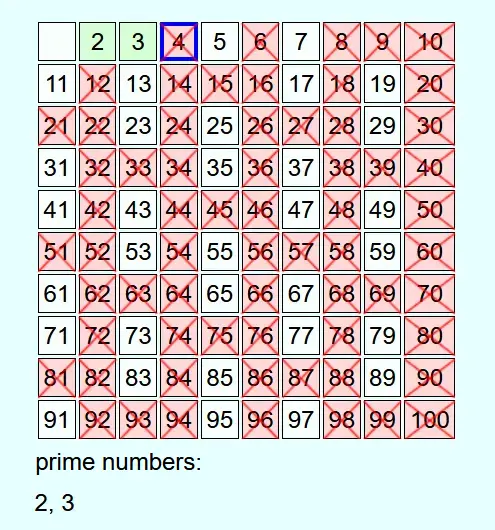
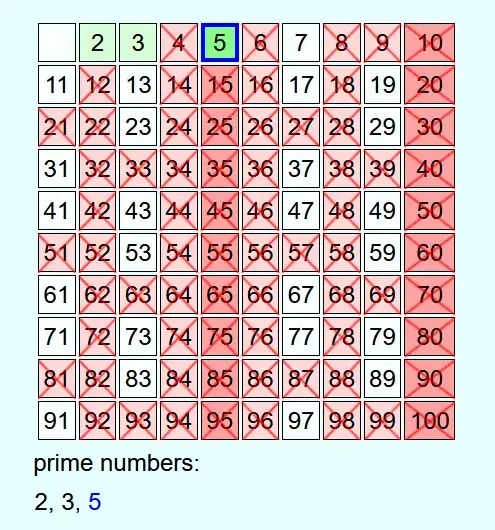
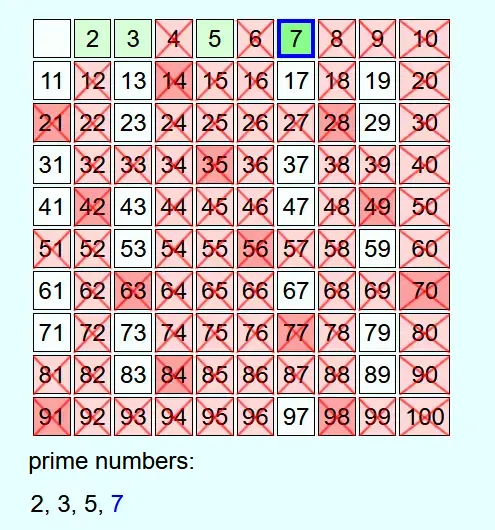
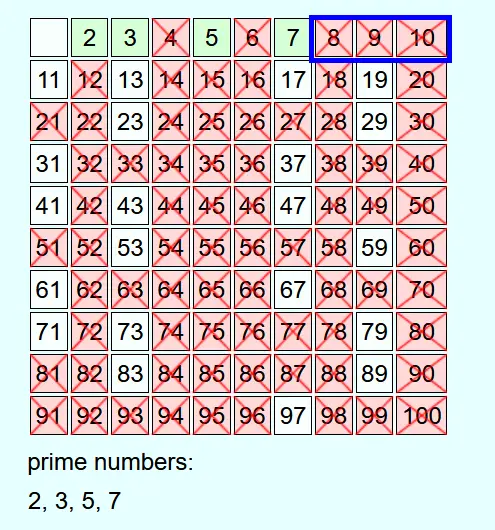
Whenever a number is not crossed out, it is a prime number. This is added to the list of prime numbers and all multiples of this prime number up to N are crossed out.
If the current number is crossed out, then it is not a prime number and nothing else is done with it.
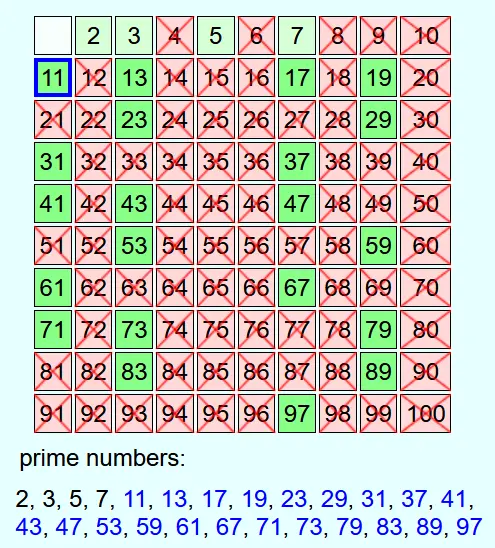
If the current number is greater than N, then all numbers up to N that are not prime numbers have already been crossed out. Therefore, the remaining numbers that are not crossed out can be added to the list of prime numbers without having to cross out their multiples.
Example
As an example, all prime numbers up to 100 are to be determined.
Reasons
Why is it not a prime number if the current number is crossed out?
If the current number is crossed out, then in one of the previous steps there was a number that is greater than 1 and less than the current number and that is a divisor of the current number. This means that the current number is not a prime number.
Why do the multiples of numbers that are crossed out not have to be crossed out?
If the current number is crossed out, then there is at least one smaller number that is greater than 1 and is a divisor of the current number. Since every multiple of a number is also a multiple of the divisor of this number, the multiples of the crossed-out current number have already been crossed out.
Why is it a prime number if the current number is not crossed out?
If the current number is not crossed out, then there is no number that is greater than 1 and less than the current number and that is a divisor of the current number. Otherwise, the current number would have already been crossed out in one of the previous steps. This means that the current number is a prime number.
Why have all numbers that are not prime numbers been crossed out if the current number is greater than N?
If you multiply 2 or more numbers that are all greater than N, you get a number that is greater than N. Therefore, the prime factorization of every number that is less than or equal to N contains at least one prime factor that is less than or equal to N. If the current number is greater than N, then all multiples of numbers that are less than or equal to N have already been crossed out. This means that there cannot be any numbers that are less than or equal to N that are not prime numbers but have not yet been crossed out.